Research
Research Overview
Jump to:
My research focuses on developing practical and rigorous statistical methods for analyzing complex, high-dimensional data using modern machine learning algorithms, particularly in settings where traditional modeling assumptions may not hold. These challenges have become increasingly important as data sets grow in scale and complexity, and as rapidly evolving artificial intelligence (AI) and machine learning models are used to drive scientific discoveries and inform decisions across a wide range of high-impact domains.
A central theme in my work is distribution-free and model-agnostic inference. These methods avoid strong or unrealistic assumptions about how data are generated or how models operate, making them especially well suited for complex, real-world applications. I have developed techniques that work in tandem with modern machine learning models to identify meaningful patterns, ensure reproducibility, and quantify uncertainty.
Because these tools are grounded in fundamental statistical principles rather than tied to any specific model or data distribution, they are broadly applicable and designed to remain relevant as AI technologies continue to evolve. This makes them particularly valuable in settings where results obtained from AI models must be transparent, trustworthy, and scientifically defensible.
Key areas of focus:
-
Reproducible Variable Selection. Determining which variables in a high-dimensional dataset are truly associated with an outcome—rather than merely correlated due to noise or confounding—is essential for interpretability and scientific validity. My work develops statistical tools that help distinguish meaningful relationships from spurious ones, enabling more robust conclusions from complex models. This is especially important in domains such as genomics, neuroscience, and biomedicine, where identifying potentially causal factors is central to advancing scientific understanding.
-
Uncertainty Quantification. Understanding how confident we can be in a model’s predictions is critical for using that model effectively and responsibly. My work provides methods to assess and report uncertainty in complex models, making AI-driven insights more reliable and defensible. This is particularly vital in high-stakes areas such as healthcare, finance, and law, where decisions based on predictions must be backed by clear, well-calibrated measures of risk.
Applied Work and Collaboration
Beyond leading my research group at USC, I serve as a consultant and expert collaborator in both academic and industry settings. I specialize in developing tailored statistical solutions, designing transparent and reproducible analyses, quantifying uncertainty in complex models, and clearly communicating statistical reasoning to diverse audiences. My work is especially relevant in contexts where flexible, data-driven models are deployed—but any errors may carry high costs and rigorous, defensible methodology is therefore essential.
Core Methodology
🔍 Reproducible Variable Selection
Modern data sets can include thousands or even millions of variables potentially related to an outcome of interest. Identifying which variables are truly relevant—rather than spuriously correlated due to noise or confounding—is a major statistical challenge. This task becomes especially difficult in high-dimensional settings, where the number of variables far exceeds the number of observations, and in heterogeneous populations, where relationships between predictors and outcomes may vary across subgroups. Addressing these complexities often requires flexible models capable of capturing diverse and subtle patterns in the data. However, if applied without proper statistical safeguards, such models are particularly prone to overfitting and can yield misleading or non-reproducible findings.
A major focus of my research is on developing distribution-free and model-agnostic tools for variable selection that can harness the predictive power of modern machine learning algorithms while ensuring reproducibility and interpretability. These methods are designed to uncover meaningful structure in complex data and to ensure that the selected variables reflect robust and practically significant relationships. In particular, I have worked extensively with the knockoffs framework, which enables powerful and flexible feature selection while controlling the false discovery rate. Because it does not rely on specific modeling assumptions, this approach is especially effective when paired with black-box machine learning models, supporting more reliable, interpretable, and scientifically defensible conclusions.
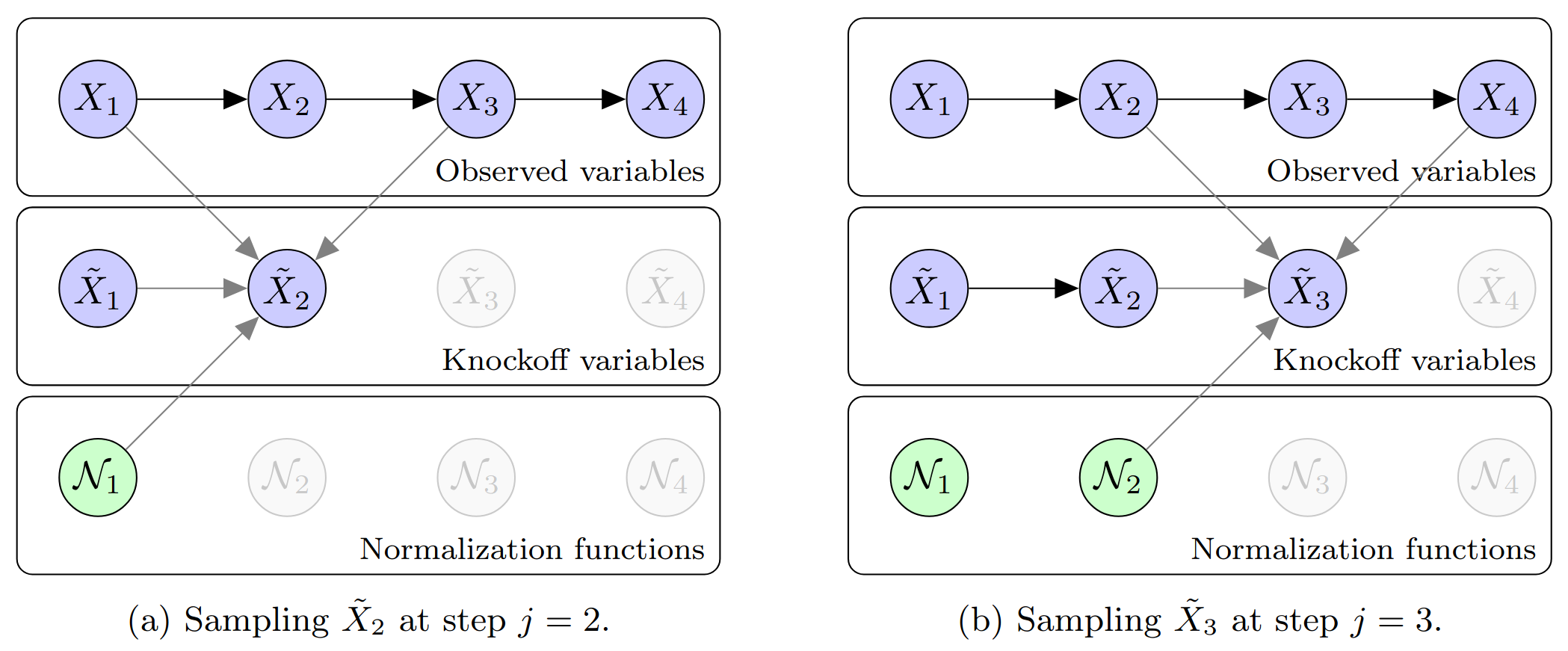
Knockoffs for reproducible variable selection in structured high-dimensional data.
This figure illustrates core ideas from my work on knockoffs for Markov chains — an early contribution to my line of work on reproducible variable selection in high-dimensional problems such as genome-wide association studies (GWAS). The goal is to identify truly associated variables while rigorously controlling the false discovery rate, even when the covariates exhibit strong sequential dependence.
The algorithm shown in the top panel constructs knockoff copies of covariates that follow a Markov chain. In this toy example with p = 4 variables, each knockoff variable is sampled sequentially using nearby original and previously sampled knockoff variables, along with an auxiliary normalization factor computed at the previous step. The result is a synthetic sequence that closely mimics the original Markov structure while remaining independent of the response — making it a valid negative control.
The bottom panel shows how knockoffs are used in practice to assess feature importance. In this example, all variables are null — none are truly associated with the outcome. The left plot shows importance scores for the original variables, which vary due to randomness, making it difficult to distinguish signal from noise. The right plot shows the same scores alongside those of their knockoff counterparts. Because all variables are null, the original and knockoff scores follow the same distribution, illustrating the role of knockoffs as a reference for controlling false discoveries.
These ideas laid the groundwork for extensions to more complex models such as hidden Markov models, and have proven especially effective for analyzing structured genomic data.
Figures adapted from: Sesia, Sabatti, and Candès (2019).
🎯 Uncertainty Quantification
Machine learning models often produce predictions without reliable information about how confident we should be in their accuracy. This lack of trustworthy uncertainty estimates can make model outputs misleading and limits their applicability in high-stakes domains where decisions must be supported by defensible statistical reasoning. While traditional statistical methods emphasize uncertainty quantification, they typically rely on rigid or unrealistic assumptions that do not hold in many modern applications—particularly when working with complex, high-dimensional data or modern machine learning models.
A central focus of my research is developing flexible, distribution-free and model-agnostic tools for predictive uncertainty, such as conformal inference. These methods can provide statistically rigorous and intuitively interpretable measures of uncertainty for the predictions produced by any machine learning model—regardless of its internal structure—without requiring strong assumptions about the underlying data distribution. This makes them particularly valuable for enhancing transparency, reliability, and accountability in AI systems used for real-world decision-making.

Understanding uncertainty in image recognition models.
This figure shows two test images from the CIFAR-10 dataset: a clean image of a ship (left) and a corrupted image of a dog (right), modified using RandomErasing to make it very difficult to recognize. Each image is processed by four different image recognition models, and their outputs are independently post-processed using conformal inference to quantify uncertainty via well-calibrated prediction sets.
A prediction set includes all labels the model considers plausibly correct for a given input — that is, labels with sufficiently high estimated probability (shown in parentheses). These sets are constructed to include the true label 90% of the time across the full test set, a property known as the 90% marginal coverage guarantee of conformal prediction.
Traditional image recognition models — especially those trained to minimize cross-entropy loss — often become overconfident, particularly on challenging or corrupted images. This overconfidence can degrade the performance of conformal prediction, resulting in prediction sets that are too large for easy examples or too small for hard ones — failing to properly reflect uncertainty when it matters most.
To overcome this, we’ve developed a new machine learning algorithm that encourages model confidence to better align with true uncertainty. By more tightly integrating model training with the conformal calibration process, our approach enables more reliable and efficient uncertainty estimation.
Figure adapted from: Einbinder, Romano, Sesia, and Zhou (NeurIPS, 2022).
📊 Data Sketching and Frequency Recovery
In some very large-scale data analysis settings, storing or processing full datasets is often computationally infeasible. In such cases, data are often compressed or summarized, which poses unique challenges for statistical inference. My work in this area focuses on recovering key signals and estimating uncertainty from compressed or lossily stored data, using sketching techniques combined with ideas from Bayesian modeling and distribution-free inference.
These methods help preserve the integrity of statistical analysis even when working with limited computational resources or streaming data. They reflect my broader goal of developing robust, principled statistical tools that remain reliable under practical constraints, and can scale with the demands of real-world AI systems.
Applied Methodology
🧬 Statistical Genetics
Understanding the genetic basis of complex traits—such as blood pressure, cholesterol levels, or diabetes risk—requires identifying meaningful associations among hundreds of thousands of genetic variants. Statistically, this poses a difficult high-dimensional variable selection problem, further complicated by the strong dependencies characteristic of genomic data, including population structure and linkage disequilibrium.
To address these challenges, I developed a statistical framework that culminated in KnockoffGWAS, a powerful distribution-free and model-agnostic method for genome-wide association studies. This approach provides rigorous false discovery rate control while carefully accounting for complex genetic dependencies. It enables reproducible, interpretable discoveries that are both statistically sound and likely to be biologically meaningful.
This line of work demonstrates how flexible inference techniques can be integrated with machine learning tools to address the scale and complexity of modern genomic data, while maintaining the statistical guarantees necessary for trustworthy scientific conclusions.
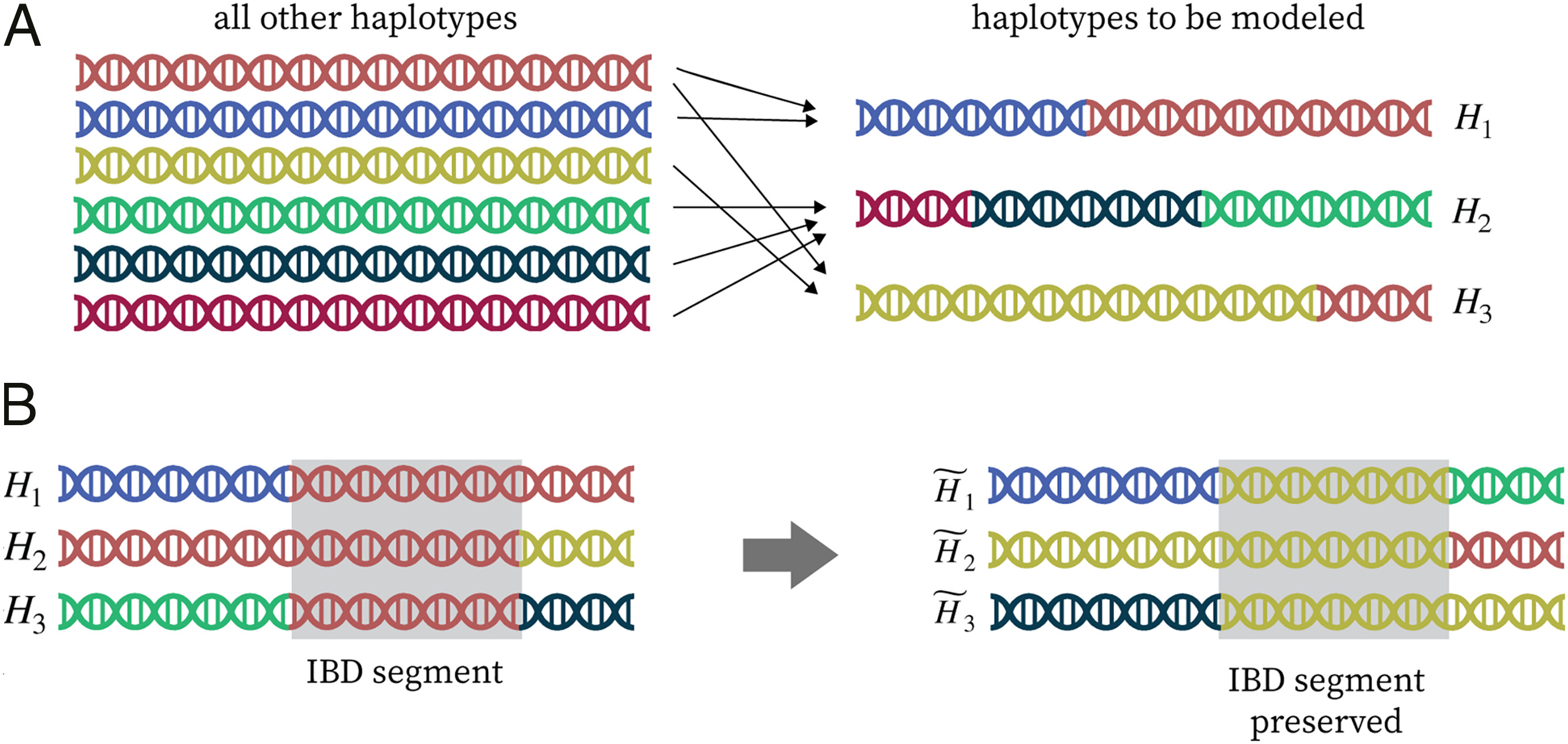
Construction of realistic knockoffs for complex genetic data.
This figure illustrates key ideas behind KnockoffGWAS, a method I developed for identifying genetic variants associated with complex traits while rigorously controlling the false discovery rate. The approach constructs knockoffs — synthetic genotypes that closely resemble real ones but are guaranteed not to be associated with the phenotype. These serve as negative controls, enabling powerful and reproducible inference even in the presence of linkage disequilibrium, population structure, or relatedness.
KnockoffGWAS builds on semi-realistic generative models of genetic variation, where the haplotypes of each individual are represented as mosaics of segments copied from others in the population — a flexible way to capture natural patterns of inheritance. These models allow us to simulate new, artificial haplotypes that are statistically indistinguishable from the originals, but provably uninformative about the trait under study.
Panel (A) visualizes this modeling framework: haplotypes are shown as sequences assembled from different reference haplotypes (in different colors), capturing shared ancestry. Panel (B) shows how knockoffs for closely related individuals preserve long identity-by-descent (IBD) segments — regions where the alleles match exactly — while remaining independent of the phenotype.
KnockoffGWAS enables scalable, transparent, and robust genetic discovery, and is implemented in fast open-source software designed for biobank-scale datasets.
Figure adapted from: Sesia, Bates, Candès, Marchini, and Sabatti (PNAS, 2021).
🩺 Biomedical Collaborations
Many biomedical datasets are messy, heterogeneous, and collected under real-world constraints. These conditions challenge conventional statistical methods and call for flexible tools that are both robust and reproducible. I have collaborated on a range of such projects involving complex patient records, clinical measurements, and diagnostic data, applying rigorous statistical inference to extract reliable insights from imperfect data.
These collaborations highlight the importance of integrating domain expertise with methodological innovation. My contributions typically involve designing customized statistical solutions in close partnership with subject-matter experts to ensure that analyses are both scientifically meaningful and statistically defensible.
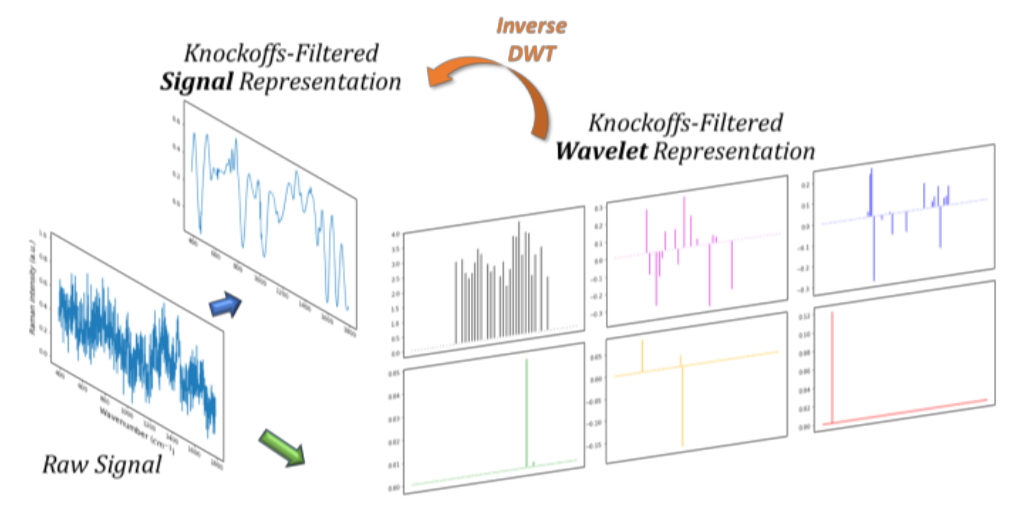
Interpretable classification of bacterial Raman spectra.
This figure illustrates key results from our work on interpretable classification of bacterial Raman spectra using wavelet-based features selected by the knockoff filter. Raman spectroscopy produces complex signals reflecting the chemical composition of samples, but raw spectral data are often noisy and difficult to interpret directly.
To address this, we transform the signals using a wavelet basis, which separates the signal into components at different scales. We then apply the knockoff filter to select a small number of relevant wavelet features while rigorously controlling the false discovery rate. These selected features are both predictive and interpretable — corresponding to meaningful chemical signatures.
The figure visualizes the selected wavelets in both the wavelet domain and the original signal domain (via inverse discrete wavelet transform). Most of the selected features are concentrated at lower frequencies, where meaningful signal dominates over noise. As a result, the reconstructed signals reveal clear peaks that correspond to distinguishing chemical bonds, which are informative for bacterial classification.
This work demonstrates that a simple, transparent model using knockoff-selected wavelet features can match the classification accuracy of complex black-box models, while providing insight into which parts of the signal matter.
Figure adapted from: Chia, Sesia, Candès, and Sabatti (2021).
🧠 Uncertainty Estimation for Language Models
Large language models (LLMs) have achieved remarkable success in recent years and are now widely used across a range of applications—including many that involve sensitive or high-stakes decisions. However, these models still make errors and often struggle to provide reliable assessments of how confident they are in their outputs. This lack of trustworthy uncertainty estimation can lead to overconfidence in incorrect predictions, making it difficult to use LLMs responsibly in contexts where reliability, transparency, and accountability are essential.
I am beginning to explore how specialized distribution-free and model-agnostic statistical inference methods can be applied to LLMs to make their outputs more transparent and trustworthy. This line of work builds on my broader research in predictive uncertainty for machine learning models, while addressing new challenges that are unique to language models—such as variable-length outputs, ambiguity in natural language, and the need for meaningful confidence measures across a wide range of tasks.
